受験生のとき模試の偏差値で一喜一憂したことはないだろうか。
偏差値を使う目的は、同じ点数でも科目の平均点により、
その価値が異なることを見分けるためだ。
例えば国語と数学で同じ70点をとったとしても、国語の平均点は70点
数学の平均点は50点だった場合、数学で70点取る方が難しいことがわかる。
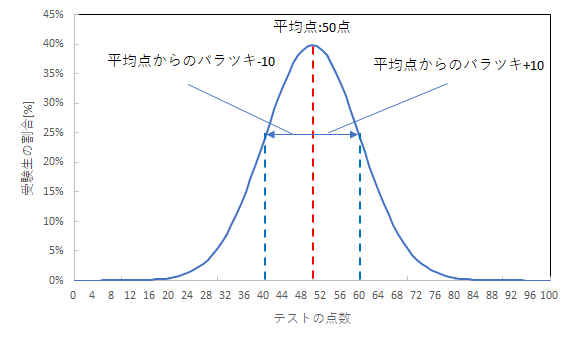
偏差値はテストの点数と受験生の割合から図.1のような
山が描けるという仮説に基づいて、式(1)から求められる。
偏差値=50+10×[(テストの点数-平均点)/平均点からのバラツキ]…式(1)
例えば、平均50点の数学のテストで70点をとったとする。
このテストの「平均点からのバラツキ」が10点だとすると、偏差値は70となる。
エンジニアはこれと同じ仮説を用いて製品の良否を判断している。
「平均からのバラツキ」の±3倍以内に製品が収まれば
どんなに大量に作って図.1の山の中に99.7%以上収まると
言うことができる。
仕事ではイメージセンサーを作るに当たり、
加工した大きさが 「平均からのバラツキ」の±3倍以内 か
どうかが一つの判断基準になる。
これを満たしていれば
同一品質の製品であることを担保できるからだ。
逆にこれを満たさない場合は、
製品のバラツキがあり問題となる。
例えば、同じメーカの同じ機種のスマホで写真を撮影したのに
片方は明るく綺麗に写って、片方は少し暗めに撮れてしまう
ということが起こり得る。
このような製品バラツキを起こさないために、
「平均からのバラツキ」という道具を使って
エンジニアは製品の品質管理をしている。
身近な具体例としてテレビの視聴率がある。
例えば「ラグビーWカップの視聴率が39.2%でした」は何を意味するか。
日本人口が1億2000万人だとすると
12000万人 × 0.392 = 4704万人
の人が見ていたという意味になる。
では、この視聴率を計算するために日本国民全員の
1億2000万人にラグビーWカップ見ていたかと聞いたのか?
答えは「NO」である。
実際には、3000世帯の家庭でのテレビの視聴実体を調査する
ことから計算している。3000世帯、およそ1万人、
1億2000万人の0.01%の調査から日本人が何を見ていたを計算している。
1万人の調査から割り出した視聴率は、1億2000万人全員を
調べて計算する実際の視聴率と多くとも0.5%しか違わない。
これは「平均からのバラツキ」の傾向から、数を多くしていっても
全体の傾向は変わらないという仮説がベースになっている。
このように「平均からのバラツキ」を上手く使うと
全部調べなくても、一部を取り出して全体を予想することができる。
参考文献:まずはこの一冊から 意味がわかる統計学
著者:石井俊全 出版:ベレ出版